Matematica per il Design – I dadi poliedrici (P. Facchini)
Marzo 22, 2022 10:54 am Lascia il tuo commentoI dadi sono uno degli elementi caratterizzanti dei giochi da tavolo, ed assieme ai mazzi di carte introducono una certa quantità di alea e di sensazione di non controllo all’interno del gioco. In questo articolo proveremo ad analizzare alcune delle loro peculiarità , delle relazioni che incorrono tra i diversi tipi di dadi, e di alcuni trucchi e segreti che nascondono le probabilità sul risultato dei dadi quando questi diventano più di uno. Tenterò dove possibile di nascondere un po’ di complessità e di tecnicismi degni di un libro di statistica, sicuramente più dettagliato di questo articolo nello spiegare formule e correlazioni matematiche di ciò che vado a raccontarvi.

Grazie alla sua forma cubica il dado più comune per una questione di semplicità di realizzazione è da sempre quello a 6 facce, ma da ormai moltissimi anni sono diventati di uso comune tutti i dadi poliedrici, ovvero quelli a 4,6,8,10,12 e 20 facce, tutti questi dadi hanno una forma di poliedro regolare nel quale ogni faccia ha la stessa forma a area di tutte le altre.
Il dado a 10 facce a volte è usato in coppia nel quale dove uno dei due dadi riporta le decine e l’altro le unità ottenendo così un dado a 100 facce o d% , il d 10 mostra i valori da 0 a 9 , lo zero viene usato con la duplice funzione di 0 o 10 in base alle necessità del caso modificando il raggio di valori da 0-9 in 1-10 , analogamente avviene la stessa cosa nel d 100 con il valore 00/0 che vale 0 o 100 a seconda della necessità di design.
Esistono dadi meno comuni, a 16 e 30 facce, oltre che i così detti “dadi dispari” a 3,5,7,15 facce , questi ultimi sono meno comuni sia per una questione di dimensione dei dadi (solitamente più grande) sia per una quesitone di distribuzione della forma del dado, che dovrebbe essere cilindrica a meno di non decidere per un dado di forma irregolare.
Solitamente i dadi poliedrici pari hanno le facce opposte tali che la somma sia sempre uguale al valore massimo del dado + 1 ( ad esempio la somma dei lati opposti di un classico dado a 6 facce è sempre 7), inoltre i numeri sui dadi vengono posizionati in modo che non ci siano tutti i valori alti e tutti quelli bassi raggruppati nella stessa sezione del dado, per prevenire che il modo in cui questo viene lanciato generare una maggiore o minore probabilità di ottenere un risultato definito.
Per mantenere una certa regolarità strutturale nella realizzazione dei dadi dispari. Altrimenti dalle forme irregolari, si usa ripetere i valori due volte, in modo da realizzare da esempio un d3 utilizzando un d6 e ripetendo le facce 1-2-3 due volte; o un d5 usando un d10 nel quale le facce da 1 a 5 sono ripetute due volte.
In base al dado che utilizzeremo cambierà la probabilità di uscita di un dato numero. È importante ricordare che quando si lancia un dado singolo indipendentemente dal numero di volte che ripeteremo la prova ogni valore è equiprobabile, cioè ha la stessa probabilità di uscita di qualunque altro.
Per quanto banale questa probabilità non si applica ad esempio nelle carte a meno di rimischiare ogni volta il mazzo, poiché la probabilità cambia in base alle carte rimaste.
Da un punto di vista di design, quindi, è utile utilizzare i dadi ogni volta che abbiamo bisogno di replicare un evento casuale in modo che le probabilità delle differenti opzioni non cambino dopo ogni lancio.
Esempio: se in un mazzo di carte ci sono 10 carte rosse e 10 blu, la prima volta che estraggo 5 carte le probabilità sono del 50-50 % , se ripeto l’operazione senza mischiare le carte appena estratte, questa ovviamente sarà diversa in base alle carte rimaste nel mazzo.
Invece lanciando un dado a 6 facce cento volte ho sempre la stessa probabilità che un dato valore esca (nello specifico il 16,67% ).
Nella tabella seguente sono riportate le probabilità di uscita di un qualsiasi numero dato in base al tipo di dado (lancio di un singolo dado):
| Dado (n. Facce) | % di successo singolo valore |
| D3 | 33,33% |
| D4 | 25% |
| D5 | 20% |
| D6 | 16,67% |
| D8 | 12,5% |
| D10 | 10% |
| D12 | 8,33% |
| D20 | 5% |
| D100 | 1% |
La probabilità di successo si somma nel caso in cui ci sia più di un risultato utile.
Ad esempio, la probabilità che su un dado a 10 facce esca un valore da 1 a 3 è uguale al 30% (ovvero alla somma delle probabilità che un numero nel range esca come risultato).
È immediato notare come alcuni dadi apparentemente “strani” siano comodissimi al momento dell’utilizzo pratico; l’esempio più classico è quello del d20 in Dungeons&Dragons, dare un bonus di +1 significa banalmente dare un +5% di probabilità di successo al giocatore, un bonus di +2 equivale al 10% e così via.
L’equiprobabilità dei risultati viene meno nel momento in cui si tira più di un dado , indipendentemente dal numero di facce ; questo accade perché il risultato non è più un valore unico ma un gruppo di valori ( ad esempio tirando 3 dadi da 6 possiamo ottenere il 3 ;6 ;1 del quale possiamo anche valutare la sua somma, 10) , questo genera una serie di proprietà interessanti. Andiamo a scoprirle.
Indipendentemente dal numero di dadi utilizzati il valore più probabile è uguale al valore medio (o ai due valori interi più vicini alla media se questa non è un numero intero) e quelli meno probabili sono il valore minimo e massimo ottenibili con quei dadi.
Prendiamo come esempio un gruppo composto da 1d10 1d6 e 1d4.
Il valore minimo ottenibile è 3 (tutti 1) , e il massimo invece è 20 (un 10 un 6 e un 4 rispettivamente) , questi valori sono ottenibili in una sola combinazione su quelle disponibili (in questo caso il totale delle combinazioni è 240). Per 2d6 il valore medio è 7, derivato da (2+12)/2, 7 è quindi il risultato più probabile tirando 2d6.
Per il gruppo di dadi in esempio il valore medio è (3+20)/2 = 11,5 , siccome il risultato non è intero, i valori più probabili da ottenere tirando 1d4,1d6 e 1d6 sono a pari probabilità 11 e 12.
Altra proprietà dei dadi poliedrici , è che il valore medio è dato da (valore minimo + valore massimo)/2 mentre normalmente per ottenere la media è necessario un calcolo più complesso.
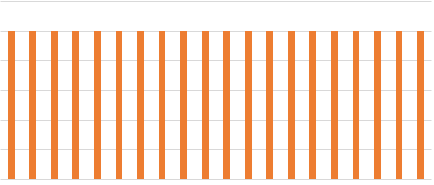
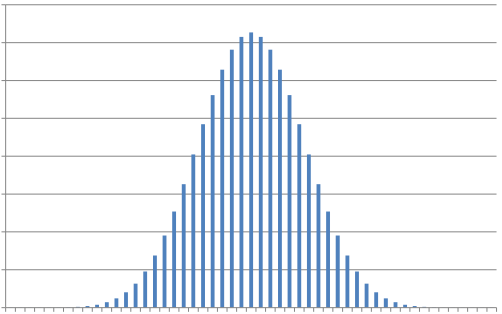
Aiutandoci con un software possiamo calcolare i vari casi probabilistici, quello che si nota è che la distribuzione delle probabilità quando il dado è uno, è una distribuzione piatta, nel quale ogni caso ha la stessa probabilità di tutti gli altri, mentre quando i dadi sono 2 o più richiama palesemente la cosiddetta Distribuzione Normale (o di Gauss) .
Nei grafici sono stati omessi i valori dei risultati nelle ascisse e delle probabilità nelle ordinate inquanto queste proprietà si applicano indipendentemente dai dadi utilizzati , i grafici sono puramente esemplificativi.
È molto facile dedurre dai grafici una ulteriore peculiarità dei dadi poliedrici : Se si lancia più di un dado, quanto più un valore è vicino al valore medio tanto più alta sarà la probabilità che quel valore esca come risultato di un lancio.
Tutto bellissimo, ma resta una domanda : Come sono state sfruttate queste informazioni nei giochi ?
Prendiamo un esempio storico. Un classico gioco coi dadi permetteva al giocatore di vincere tirando un 3 o un 18 su 3 dadi da 6 con pagamento doppio nel secondo caso e di perdere tirando un 10 o un 11. Il gioco continua fino a quando uno di questi valori esce.
Apparentemente il giocatore ha 2 combinazioni vincenti e 2 perdenti, ma per ciò che abbiamo appena affermato sappiamo che :
Tirando 3 dadi a 6 facce, sia il valore minimo 3 che il valore massimo 18, hanno una sola combinazione possibile ciascuno, e una probabilità di uscire di 1/216, mentre i valori medi (10 e 11) hanno parecchie più combinazioni possibili ovvero 27/216 , quindi di fatto, il giocatore aveva una 2 probabilità su 216 di vincere (0,9%) , contro le 54 su 216 (25%) di perdere con ciascun tiro.
Bastava per il banco conoscere le proprietà dei dadi per vincere molto più spesso dei giocatori. Se volete un motivo per il quale definire il 666 come il numero del diavolo … beh…. l’avete trovato.
Un altro esempio utile è Coloni di Catan, dove l’evento più probabile su due dadi, ovvero che la somma dei due dadi sia 7 genera l’unico evento che non fa produrre risorse (i banditi). E’ molto probabile che questo valore sia stato scelto come generante l’evento dei banditi proprio affinché capitasse abbastanza di frequente (mediamente una volta ogni 6 turni) e generasse dinamiche interessanti ai fini del gioco tra i giocatori al tavolo.
Analogamente i giocatori che posizioneranno le loro città nei nodi adiacenti ai numeri più vicini al valore medio (il 6 e l’8) statisticamente riceveranno più spesso risorse rispetto a chi ha posizionato le città su nodi adiacenti a numeri più lontani dalla media (su tutti 2 e 12).
In Stone Age, in base al numero di dadi lanciati, è abbastanza semplice calcolare il valore medio , e quindi la quantità di risorse mediamente ottenibili in un turno da un giocatore sulla base di quanti lavoratori ha speso, e a bilanciare tutto di conseguenza. È interessante vedere quanto conoscere questa informazione mostri l’armonia del bilanciamento nel design dei costi delle risorse e dei relativi punteggi per le capanne.
| Dadi lanciati | Risultato medio dei dadi (somma) | Cibo | Legno | Argilla | Pietra | Oro |
| 1 | 3,5 | 1 | 1 | 0 | 0 | 0 |
| 2 | 7 | 3 | 2 | 1 | 1 | 1 |
| 3 | 10,5 | 5 | 3 | 2 | 2 | 1 |
| 4 | 14 | 7 | 4 | 3 | 2 | 2 |
| 5 | 17,5 | 8 | 5 | 4 | 3 | 2 |
| 6 | 21 | 10 | 7 | 5 | 4 | 3 |
| 7 | 24,5 | 12 | 8 | 6 | 4 | 3 |
Infine, diamo un’occhiata a Dungeons & Dragons. Tirando 3d6 per definire il valore delle 6 caratteristiche principali, il valore medio è 10,5 … casualmente (ma ora sappiamo nemmeno poi tanto) i designers del gioco hanno deciso di assegnare alla coppia di valori 10 e 11 l’assenza di modificatori alla caratteristica; aumentando e diminuendo l’entità del modificatore via via che ci si allontana dal valor medio. Interessante per noi diventa valutare il fatto che per migliorare l’esperienza di gioco e dare l’impressione al giocatore che il proprio personaggio sia effettivamente “eroico”, è diventato uso comune al punto da essere citato nei regolamenti il lanciare 4d6 e scartare il valore più basso. Questo ha alzato la media dei risultati a circa 12,5 facendo sì che i giocatori incorressero più spesso in modificatori positivi migliorando la percezione della “forza” del proprio personaggio.
Mi auguro che questo piccolo excursus nel mondo dei numeri non vi abbia turbato troppo e che magari diventi occasione e spunto per qualche idea interessante per i vostri giochi. Buona invenzione !
Categoria: Senza categoria
Questo articolo è stato scritto da Khoril
